应用“房室模型”动力学认识新型冠状病毒肺炎(COVID-19)爆发期的传播规律
2020-04-19 22:22:20 浏览:21368 来源:
摘 要:新型冠状病毒肺炎(COVID-19)从2020年1月下旬开始大规模爆发,COVID-19动力学建模的相关报道认为建立合适的数据收集体系并科学处理海量的信息对于疫情控制非常重要。不论是从理论上还是在实践中,该类非线性流行性疾病的传播和治疗都受到多种因素、多个层面以及不同防控措施的影响。在确证了存在“人传人”的传播途径之后,分析武汉封城后1~40 d我国以及全球疫情大爆发初期的感染人群数据确诊病例和新增病例的数据变化规律。我国迅速采取了“封城”“隔离”和“带口罩”等控制病毒传播的措施,并取得阶段性成功。为科学判定传染病危害程度,提出简化的“传播相”和“处置相”的“二房室”模型,并基于国内和国际疫情数据予以分析。病毒传播速度研究传播爆发期的动力学分析对控制疫情爆发更具有实际意义。全球防疫咨询中心和世界卫生组织(WHO)的总确诊人数和现有确诊人数的传播速率(Kt)和倍增时间(tt2/1)基本变化不大。研究发现全球传播tt2/1均明显短于我国的6.27~7.02 d,表明全球的传播速率明显高于我国。注意到意大利、西班牙和伊朗3个国家总确诊人数的Kt、tt2/1和死亡率均与全球数据有明显差异。特别是死亡率明显高于全球水平,分别为9.57%、6.59%、7.86%,约为全球的2倍,是我国的3倍。因此,研究认为处理好传播途径和控制传播速率是关键。
数学模型成为解释传染病流行病学的一种重要模式,通过建立合理的数学模型对传染性疾病发展趋势和控制的预后进行预测和研究,能够为整体防控决策的制定和评估提供非常有价值的工具[1-7],同时也为认识传染性疾病流行规律和面对复杂因素而采取适当的干预措施提供了极大的帮助。新型冠状病毒肺炎(COVID-19)出现,并在2020年1月下旬开始大规模爆发,从网上检索到COVID-19动力学建模计算的相关报道,这为传染病的防控提供了一定的帮助和参考[8-14]。然而如何建立合适的数据收集体系并科学地处理海量的信息,是目前面临的实际困难。理论上和实践中,该类非线性流行性疾病病毒感染者的传播和治疗受到了多种因素、多个层面以及防控措施的影响,如不同年龄结构、不同人群基础健康状况不同,见图1、2,数据均来源于中国疾病预防控制中心。人群的敏感程度、症状是否出现、症状的轻重程度、机体免疫能力也存在显著的差异,另外还包括病原生物学、病毒进化、人类行为因素等的影响。
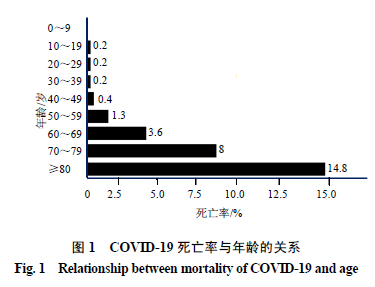
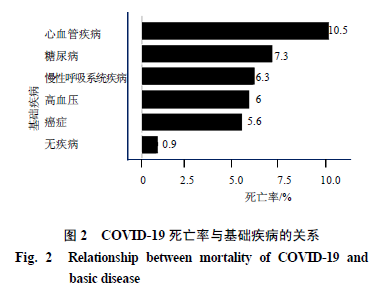
世界疫情正在向着尖峰型曲线形态发展的概率上升。居高不下的死亡率和快速上升的确诊率,其原因推断为检测不足,世界疫情数量仍有低估,还与患者没法得到检测和认定有关,整体疫情还在迅速上升期,高峰仍然在前。这一切都预示一个全球疫情的爆发正在到来。疫情的最终结束,第一取决治疗药物的研发,第二取决于疫苗研发成功。因此疫情变化将影响世界控制疫情发展的时间。世界卫生组织(WHO)面对疫情形势,认为只有全球、各国政府和社会大众高度协作,通力合作,才能缩短疫情时间,减少疫情损失。
1 经典传染病动力学数学模型
1.1 SIR房室模型
传染病建模计算早在20世纪初在黑死病流行时,SIR房室模型是用于流行病动力学研究的经典的和最基本的模型,为传染病动力学的研究奠定了基础。
该“房室模型”的基本假设:一是人群混合良好,所有接触者都有相同的可能性;二是只需记录不同状态或区域的宿主数量。典型状态下宿主可划分为:(1)易感染者是指尚未患病但缺乏免疫力、与感染者接触容易受到感染的人群;(2)感染者是已经受到疾病感染的人群,并且可以传播给易感染者;(3)恢复者(或移除)是死亡或因为病愈而具有免疫力的人;(4)暴露者为“已接受到感染”,但未被感染;(5)病毒(菌)携带者为“被感染”能够传播疾病,但传播概率不确定。
基于以上分析,该模型中把传染病流行范围内的人群分成3类:(1)S类为易感者(Susceptible),指未得病者,并缺乏免疫能力,与感病者接触后容易受到感染,此数值难以准确估算;(2)I类为感病者(Infective),它可以传染给S类成员;(3)R类为移出者(Removal或Recovered)是指被隔离者和因病愈而具有免疫力的人。在若干假设下,模型导出S、I、R 3个函数的微分方程组。根据已有数据得到的拟合曲线并外延,进行疫情预测。
通过多种形式的传染病模型研究时,其模型结构和方法的选择应由所研究问题和信息的来决定,一些简单和复杂的数学模型模型已被证明可用于研究疾病动态、预测疾病发展趋势,进而影响控制政策的制定。但是,SIR模型只能对疫情进行定性预测,很难给出准确的预测值。很多传染病学者提出了其他更加复杂的模型,并尝试将建模计算数据与病例统计数据进行更好的拟合,然而这并不是件容易的事情。
根据已有数据得到的拟合曲线并外延,进行疫情预测。由于传染病模型可能有多种形式来研究,其结构和方法应由研究问题和信息的可利用性决定,简单和复杂模型已被证明可以了解疾病动态、预测疾病趋势,并可以影响政策的控制。但是,其只能对疫情进行定性预测,给出定量预测值困难,或偏差大。很多传染病学者提出了其他模型或更复杂模型,尝试建模希望计算数据与病例统计数据拟合更接近。
1.2 SARD模型
在SARS期间,利用数学模型得出了传染病增长率、传染病倍增时间和基本再生数(R0),R0定义为在无另外感染的人群中,一个病例在其传染期间平均可传染的病例的预期数量。对于由一人传至另一人的间隔时间,使用的信息先验分布是基于SARS由一人传至另一人的间隔时间(均值为8.4±3.8)[15]。在此次疫情初期,利用MATLAB软件(MathWorks)对潜伏期、由一人传至另一人的间隔时间、增长率和R0进行分析。如估计R0=2.2,这意味着每例患者平均将感染传给了另外2.2人。如估计R0=3,这意味着每例患者平均将感染传给了另外3人,平均潜伏期为5.2 d,95%置信区间(CI),为4.1~7.0,潜伏期为12.5 d。在初期,倍增时间为7.4 d。由一人传至另一人的平均间隔时间为7.5 d(CI,5.3~19),R0估计为2.2(95%CI,1.4~3.9)[16]。
有研究的目标是寻找疫情关键函数的解析解,参考前人的模型,有作者反复思考和在计算机上定量计算试验,提出传染病动力学SARD新型模型,并提出痊愈率(γ)是逻辑回归函数,一个大胆但合理的假设[17],模型中4个函数,S、A、R、D有解析解,并用于COVID-19疫情定量分析和预测。
SARD模型中4个函数S、A、R、D,分别称为易感者、累计感病者、累计痊愈者、累计死亡者。现有感病者函数I不包括在模型方程内。SARD模型中γ和死亡率(δ)定义如下:
累计痊愈者R=γ×A
累计死亡者D=δ×A
每日新增感病B=当天累计感病者A数-前天累计感病者A数
现有感病者I=A-R-D
这里SARD模型中的γ与SIR模型中定义不同。在若干假设下,推导得到SARD模型中的4个函数S、A、R、D的一阶微分方程组。求解A的一阶微分方程,得到了累计感病者函数A的解析解,是逻辑回归函数。另外,本模型提出一个大胆但合理的假设,γ也是逻辑回归函数。δ可以采用疫情数据的线性函数拟合,得到δ函数的两个参数。线性函数一次方系数等于零,对应为δ采用疫情数据平均值。
因此,采用SARD模型,选取传染病疫情5~11 d的累计感染者A、痊愈者R和死亡者D的数据,在传染病疫情期间的关键数据全部可以计算得到,并可进行定量疫情预测,给出累计感染者A、新增感染者B、痊愈者R、死亡者D以及现有感病者每天数量。采用SARD模型计算也可计算得到疫情的其他参数。如R0,只要知道传染者传染周期就可计算得到。R0=β/γ≈传播率/恢复率,为完全易感人群中平均原发病例引起的平均继发病例数。R0=1时的流行病阈值即易感物的比例必须超过(γ/β-R0-1),R0必须足够小,否则就可能出现疾病传播。
1.3 SARD模型用于COVID-19早期疫情分析
2019年12月COVID-19流行病爆发以来,国内外的流行病、统计学及其他专业学者进行了大量建模计算和疫情分析预测。利用SARD模型,计算得到COVID-19流行病疫情主要数据与通报数接近,表明模型适用于这类流行病的分析。因而定量预测疫情发展趋势数比较可靠。
1.3.1 湖北疫情分析 湖北地区建模计算采用2月13~17日(5 d)数据,预测累计感染者总数65 000人,相对偏差3%。在1月24~26日的3 d内R0=3.6±0.3。但是,在2月12~13日期间,R0<1,偏差1 d。传染周期选用12 d。预测现有确诊人数拐点区在2月17~19日,最大人数5万人,偏差3%。疫情末期痊愈率达96.3%左右。预测死亡人数2 300人左右。
1.3.2 湖北以外疫情分析 建模计算采用2月4~14日(11 d)数据。(1)预测累计感染者总数13 000人,相对偏差3%。(2)在1月24~26日的3 d内R0=2.8±0.3。在2月6~7日,R0<0,日期偏差1d。传染周期选用12 d。(3)疫情预期在3月6~7日走向尾声,那时现有确诊人数小于500人。很多地级市现有确诊人数将清零。(4)疫情末期痊愈率达98.6%左右也偏高,而预测死亡人数140人左右则偏低。
通过SARD模型计算,就可计算得到早期的R0。从已经发表的论文中看出,选用疫情早期通报数据,计算得到的R0往往偏差大。R0是传染病群体生物学的重要参数,它取决于病原微生物在个体宿主循环周期、病原微生物释放数量与期限、病原微生物抵抗力、传染程度、宿主行为、卫生条件和干预、群体免疫状况等影响。R0受社会因素、自然因素和病原微生物的生物学特性影响。因此同一种病在不同的国家和不同的时期及同一国家内均不同。以不同作者基于数据来源所计算的,或从不同研究分析所得资料相同疫情得到的R0的差异大。
2 “二房室”模型的基本概念
“房室”(compartment)动力学数学模型是许多动力学研究的常用模型,如药动学的“一房室”(one compartment)模型、“二房室”(two compartment)动力学、“三房室”(three compartment)动力学模型等“多房室”药物动力学研究。是否也可以广泛应用于传染病流行的动力学模式分析值得探讨。
任何病原体会直接或间接在不同个体之间直接传播、在不同种属(动物与人,人与人)的宿主间传播,或在环境中长期存活,人群在病毒接触过程中,一部分人群感染后出现一定时间的潜伏时间,以一定速率感染后发病、疾病进程和危害程度不同,有的获得免疫而不发病,有的治疗后能痊愈,有的病情加重,甚至死亡。在疫情爆发后,敏感人群(S)感染后使一部分人成为感染者(I),一部分人获得免疫或自愈和治愈(R),这3部分人数随着时间幻化形成如图3的变化规律。而衡量病毒感染的感染人数的变化是认识其传播速度和康复的基本曲线。本文主要研究疫情爆发期感染者的快速增长的曲线变化规律。
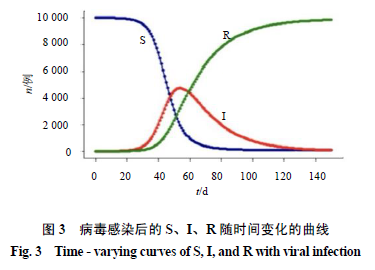
以上变化过程及其规律分析可以用“二房室”动力学模型来模拟,将全过程简化成病毒“传播相”(transmission phase)和“处置相”(disposition phase),见图4。
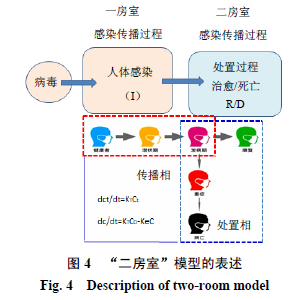
在传播相,由于潜伏期后进入爆发期,其感染人数会快速增长,利用高峰值之前的数据计算其传播速率和倍增时间。高峰值后进入处置相,其感染人数随着部分患者自愈、治愈或死亡,所剩余人数在渐渐减少,用此模型分析获得处置速率和治愈速率或死亡率。通过此模型可以简便地获得感染传播和处置的有关信息,有利于认识流行病的发展规律,也可以用于预测和预后分析。
一般经过一定时间的潜伏期如2周,开始病毒感染和传播。图5为流行病传播病例数和感染后经过治疗处置的病例数随时间变化的示意图。当无防控干预时,传播速度极快,很快达到传播峰值时间(tmax1)和出现大量患者(Cmax1),高峰过后大部人具有群体免疫水平,而一部分患者由于无免疫能力而死亡,所存患者数量也快速减少。当有强大防控干预时,传播速度较慢,达到传播峰值时间(tmax2)延长,感染人数减少,其峰值明显低于无防控干预条件下的人数(Cmax2),高峰过后大部人获得救治,康复出院,获得免疫能力,死亡数量也随之减少。
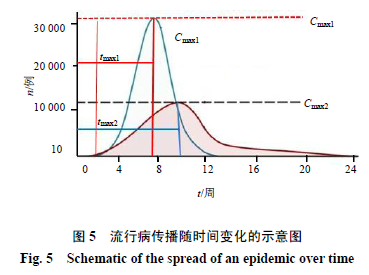
这两种情况下的感染人数随时间的变化规律,在传播爆发期的传播过程,病毒感染后被感染人数和处置过程中实际人数的指数函数关系,它由两部构成:
dct/dt=−KTCt
dc/dt=KTC0-KeC
可以认为任何时候的感染人数可用以下指数方程表示:
Ct=A(e−KTt-e−Ket)
如何去控制传染病传播中的关键事件,面临的困难包括感染病例的低报告率、防控措施影响因素、以及对人对病毒认识和应对措施的理解,如何评估其在人与人之间传播的可能性,同时分析其进化为致病性更高菌株的风险性能力。还有许多因素如日趋严重的抗菌素耐药、人类间相互联系的频繁、人口增加和流动、城市化与环境和土地使用的变化以及人们行为等因素都给传染性疾病的防控带来挑战。
提高对传染病以及生态系统中的传播动力学的理解是解决问题的关键,它不同于随机混合的简单假设。在基于不完整的数据(如敏感人群数量和处置过程的多因素变化)进行模型参数的预测,或是将模型结果与实际观察结果比较,均显示现有模型的有不足之处。笔者认为根据确诊人数和新增人数的病例数与传播时间的关系,还可以引入传播速率(Kt)和传播倍增时间(tt2/1)两个参数。这两个参数同样可以评价发病率、死亡率和治愈率为基础的疫情监管系统的科学性。在感染爆发期,感染人数增值速度远远大于治愈和死亡速度时,其Kt可以简化认为是传播量(C)与时间(t)的函数(dc/dt=KtC),Kt计算公式为:
Kt=[(lnC2)-(lnC1)]/(t2-t1)
或Kt=2.302 6 [(lgC2)-(lgC1)]/(t2-t1)
tt2/1是衡量传播速度的另一参数,可用以下公式计算:
tt2/1=0.693/Kt
3 应用“二房室”模型计算Kt和tt2/1
3.1 武汉封城后1~40 d确诊病例和新增病例的数据变化规律
国家卫生健康委员会公布的武汉封城后的1月23日—3月2日的40 d的每日累计确诊病例人数和新增人数的动态变化数据见表1。按10 d为1个周期安排数据,发现每个周期与前个周期的最后1d比较均出现1个谷值。经过此谷后又开始,其新增人数又按顺序增长,图6和图7能看到这个谷值的出现。是否可以认为其病毒传播规律为10 d一个周期呢?
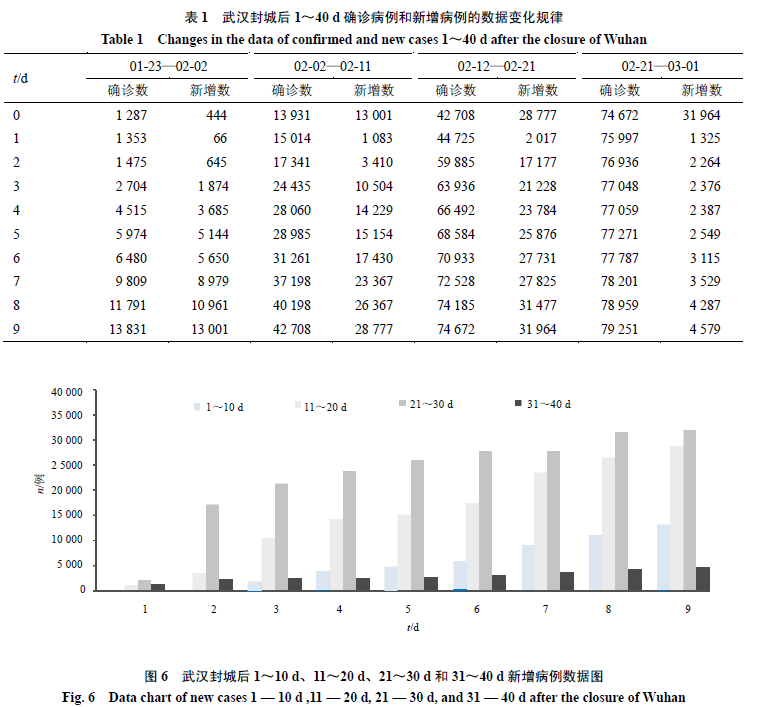
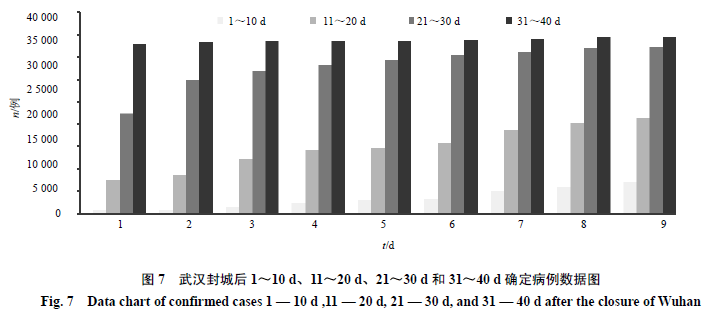
有关流行病学者和公众非常关心拐点问题。流行病统计学通常把现有确诊人数最大日作为拐点,现有确诊人数在最大日期的前后一天,差别比较小,另外流行病统计数量也有一定偏差。根据2020年1月23日武汉封城后,国家卫生委员会发布的1月23日—3月2日40 d的每日累计确诊病例人数见图8。从此曲线可见,封城后10d出现明显的确诊人数较快上升的第1个拐点,到30 d出现确诊人数平稳上升的第2个拐点。30~40 d,确诊人数呈现平台状态,新增确诊人数日渐减少。对不同时间区间(2月2日—2月16日和2月17日—3月2日)各2周的累计确诊人数,现有确诊人数、治愈人数和死亡人数(其中现有确诊人数为累计确诊人数减去累计死亡患者和累计治愈人数之差)4项进行统计分析,按本文给出的方法计算传播的Kt、tt2/1、死亡率或治愈率,见表2。
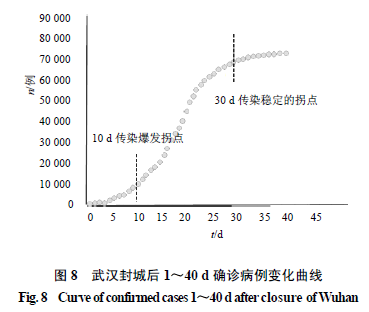
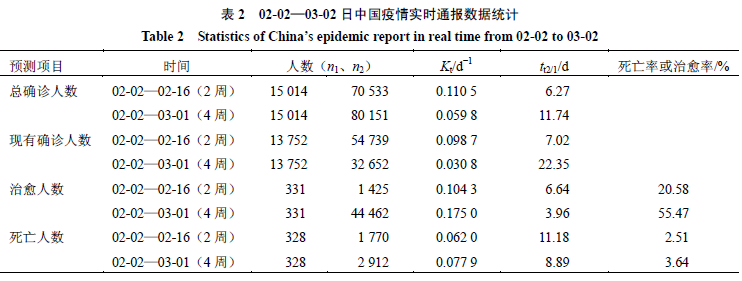
由表2发现总确诊人数在前2周的Kt为0.110 5/d,其传播人数的tt2/1为6.27 d。由于后期治疗及时、得当,特别是中医用药治疗介入,确诊人数增速放慢,4周的Kt为0.059 8/d。由2周的治愈率20.58%,提高到4周的55.47%。在2周和4周的死亡率分别2.51%、3.64%。
3.2 全球疫情大爆发初期的感染人群数据的分析
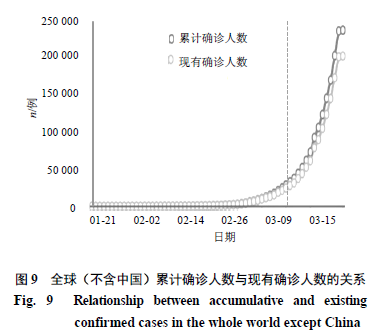
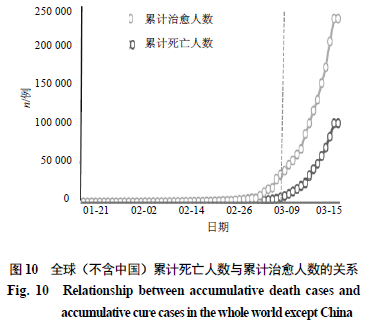
根据WHO和全球防疫咨询中心(GlobalConsultation and Prevention Center)网上公布的全球2020年1月21日—2020年3月23日的数据,对确认感染人数和死亡人数进行分析。图9显示全球(不含中国外)累计确诊人数与现有确诊人数的关系。图10显示全球(不含中国外)累计死亡人数与累计治愈人数的关系。
根据WHO和全球防疫咨询中心网上公布的全球2020年3月9日—3月23日的全球(不含中国外)的数据。对不同时间区间的累计确诊人数,现有确诊人数、治愈人数和死亡人数(其中现有确诊人数为累计确诊人数减去累计死亡病人和累计治愈人数之差)4项进行统计分析,见表3。
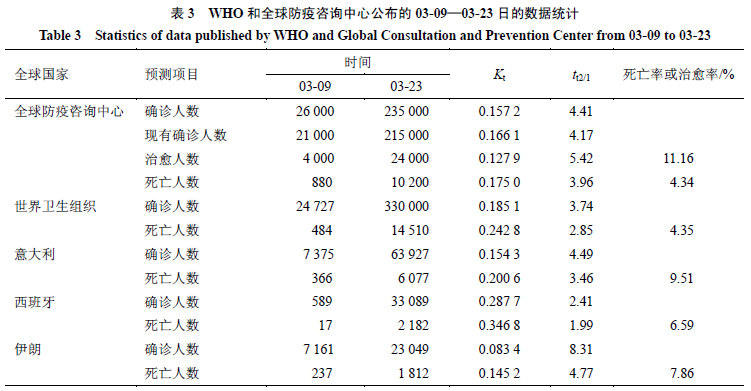
从表3中可以看到来源于全球防疫咨询中心和WHO的资料,两来源的总确诊人数和现有确诊人数的Kt和tt2/1基本变化不大,分别为0.157 2/d和4.41 d、0.185 1/d和3.74 d。但是,其tt2/1均明显短于我国的6.27~7.02 d,表明全球的传播速率明显高于我国42%~80%,说明其传播速率明显快于中国。其死亡率分别为4.34%、4.35%,也比我国的高20%~30%。
注意到意大利、西班牙和伊朗3个国家的总确诊人数的Kt、tt2/1和死亡率均与全球数据有明显差异。特别是死亡率明显高于全球水平,分别为9.57%、6.59%、7.86%,约为全球的2倍,是我国的3倍。
4 讨论
4.1 传播速度是判断感染危害的重要因素
判断传染病危害的4个主要因素——病原体、传播途径、传播能力和死亡率都存在不同程度的不确定性。在比较乐观的情况下某1个因素不确定,在不乐观的情况下则可能4个因素都不确定。在这次COVID-19疫情中,病原体被确定了,但其他3个因素到目前为止都还有不同程度的不确定性。公共卫生系统的一个主要任务是及时控制住各种危害人类的病原体在人间的流行,不要形成危害社会的重大疫情,形成严重的公共卫生危机。面对该疫情,武汉封城以后出现明显转机是值得肯定的。在此后的近40 d,有效地防控局面,在很大程度上降低了传播速度和对公众的危害。不同国家对WHO的“警钟”得到重视程度的差异,也反映了拖到今年3月所形成的COVID-19疫情在全球大流行的结果。
4.2 中国采取的“封城”“隔离”和“口罩”在防控中的作用
病原体传播途径的确定也是能否控制传染病危害的关键一环。在忽视了要去防止“人传人”的时候,并没有认识到“封城”“隔离”和“口罩”在控制快速传播中的重要性;特别是在交通快速发达的流动社会给快速传播提供了条件;还有科学技术的发展,对处置传染病也会带来不同的结果,依据100年前人们对传染病传播的认识来评价和预测,其中的未知数影响结果的可靠性,甚至出现失误。在流行病学领域,判断一个传染病的传播能力通常是采用R0,即在一个封闭条件下,没有外力介入和所有人都没有免疫力的情况下,一个感染到某种传染病的人,会传染给多少人的平均数。
4.3 基于疫情判断,控制传播速度是第一要素
防止传染病危害的决策主要考虑对疫情性质(传染性、危险性)判断、防控措施和治疗实施3件事的特征认知,不同国家、民族和文化背景因素有着巨大的差别,甚至截然不同。但对传染病危害程度的判断特别需要考虑4个因素:病原体、传播途径、传染能力和死亡率的科学判定极具挑战性。新冠病毒肺炎的R0目前有不同的数值,有人说“3”,在早期说是“2”,在爆发期更大,如果没有控制,该传染病会以指数方式传播的数学模型处理,会有不同可能的数值。有外国专家认为,这个病在感染初期最具传染性,特别是刚出现症状的2~3 d,但新冠病毒感染者7 d之后传染力会急剧降低。还需要强调的是,传染力将随着外力介入的时间和强弱发生巨大的变化,尽管治疗决策中,由于人体和疾病的复杂性、人类知识以及医疗技术等方面的局限性。因此按照治疗方案实施的效果是不确定的,可能有效,也可能无效;可能出现副作用,也可能不出现副作用。特别是2月以来,对患者“应收尽收”和中医药的介入,其决策付诸临床实践,改变了医生和患者还要面对的不确定性。也就是说,针对诊断清楚的疾病,大大提高防控效率。
4.4 死亡率是判断传染病危害大小的决定因素
如果一种传染病的致死率很低,那么就不一定花费巨大的人力和物力去进行控制,反之则需要下大力气。世界许多国家的府官员和流行病专家一直把COVID-19疫情的死亡率等同于季节流行性感冒的死亡率。然而传染病的死亡率高低是一个复杂的问题,涉及到许多方面。国家的卫生资源和水平显然是很重要的。德国卫生部长施潘就认为,在德国COVID-19的死亡率将在0.1%~0.7%,美国在1%左右。本文通过WHO和国际数据库提供的信息,计算得到意大利高达10%,伊朗和西班牙的病死率也攀升至6%以上的结果。疾病的进程变化也是需要考虑的。我国在2%~3%,而COVID-19重症比例至少是10%~20%。死亡率随着传染病的传播程度会发生改变。它与各国各地区的医疗水平和年龄结构和基础健朗状况有关。
5 结论
基于疫情判断,控制传播速度是第一要素。在交流、交通快速发达的流动社会给快速传播提供了条件。认知“人传人”之后,我国“封城”“隔离”和“口罩”在控制快速传播的措施严。也就是说,对传染病危害程度的判断特别需要考虑4个因素:病原体、传播途径、传染能力和死亡率的科学判定,处理好传播途径和控制传播速率是关键。所以,本文重点研究放在图1所示传播爆发期的动力学曲线上升速率的分析。提出简化的“传播相”和“处置相”的“二房室”模型。
全球防疫咨询中心和WHO的总确诊人数和现有确诊人数的Kt和tt2/1基本变化不大,分别为0.157 2/d和4.41 d、0.1851/d和3.74 d。但是,其tt2/1均明显短于我国的6.27~7.02 d,表明全球的传播速率明显高于我国42%~80%。其死亡率分别为4.34%、4.35%,其死亡率也比我国高20%~30%。注意到意大利、西班牙和伊朗3个国家总确诊人数的Kt、tt2/1和死亡率均与全球数据有明显差异。特别是死亡率明显高于全球水平,分别为9.57%、6.59%、7.86%,约为全球的2倍,是我国的3倍。这些差异与我国采用多种隔离措施和中医药介入等综合治疗措施有关。
参考文献(略)
来 源:刘昌孝,王玉丽,张洪兵,武卫党. 应用“房室模型”动力学认识新型冠状肺炎(COVID-19)爆发期的传播规律 [J]. 现代药物与临床, 2020, 35(4).

